フィボナッチ数の謎。
読み解けば相場の秘密がわかるかも知れません。
この数列は黄金比の計算の元となるもので、自然界のあらゆる事象に含まれていると言えます。
フィボナッチ・リトレースメントがトレードの一助となるのでしょうか?
その特徴・使い方をまとめました。
フィボナッチ数列とは
簡単に言うと「前の2つを足した数が、次の数になる」数列です。
数学上の定義は、シンプルな漸化式(ぜんかしき、数列を表す文字式)で表せます。
実際のフィボナッチ数列
0 (第1項)
1 (第2項)
1 (第3項)
2 (第4項)
3 (第5項)
5 (第6項)
8 (第7項)
13 (第8項)
21 (第9項)
34 (第10項)
(以下続く…)
フィボナッチ数列の覚え方
フィボナッチ数列は、最初の項が0、次が1です。
なぜ最初が0で、次が1なのか?
そう考えると話が進みませんので、最初の2項についてはそういうものだと思うしかありません。
(数学上の初期条件。)
第1項が0、第2項が1、第3項は「前の2つを足した数」。
したがって第3項は1です。
第4項も「前の2つを足した数」。
つまり、第2項と第3項を足して第4項は2。
第5項以降も同じやり方で、永遠にフィボナッチ数列は続きます。
フィボナッチ数列が世を席巻する
ひまわりの種の並び方
ひまわりの種。
右回り、左回りのらせん状に並んだ種の列。
この一列の種を数えると、必ずフィボナッチ数列の数になっています。
松ぼっくりのかさ
ひまわりと同じく、1列のかさを数えるとフィボナッチ数列の数です。
木の枝分かれ
私が描いた木の枝です。
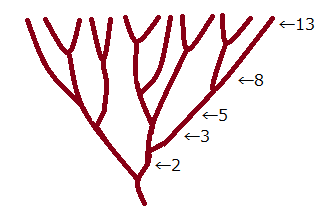
枝分かれの数を調べると、見事にフィボナッチ数列の数になっています。
自然界でも、このような枝分かれになっている例は少なくありません。
絶対にこの通りになると言う訳ではありません。
しかし、何かが世の中の全てを運命づけている気がしなくもありません。
その何かとは…?
枝分かれのルールを定めれば全てが運命づけられる
- 必ず2つに枝分かれする
- 強い枝が先に枝分かれする
- 弱い枝は次に枝分かれする
この規則のもとに枝分かれさせると、枝分かれの数は必ずフィボナッチ数列の数になります。
最初に何かが決まった時点で、あらゆる運命が規定されてしまっているかのように。
その他にも
- 台風の渦巻き
- 巻き貝の断面図
- 葉脈の枝分かれ
など、自然界のあらゆる場面で出没する謎の数字。
それがフィボナッチ数列です。
フィボナッチ比率とは
フィボナッチ比率とは、フィボナッチ数列各項の間の比率です。
【例】直前・直後の項の比率
前の項を後の項で割ると、例えば
(第7項)÷(第8項)
=8÷13
=0.61538461…
この比率を全ての項について調べていくと、ある一定の数値が浮かび上がります。
0.61803…
この数値がフィボナッチ比率の例。
フィボナッチ比率は、隣り合った項だけではなく、飛び飛びの項その他、いろいろな数値が存在します。
フィボナッチ比率は、黄金比率の謎を解き明かす鍵にもなっています。
黄金比とは
隣り合ったフィボナッチ数列の比は、黄金比そのものだと言って過言ではありません。
長方形の縦横比においても、最も美しい比率とされます。
その比率は 1:1.618 です。
世のあらゆる美貌の持ち主、そのお顔もこの比率なのだとか…。
モナリザの微笑みも黄金比率です。
黄金比を株のトレードにどう生かす?
これらの数列や比率、黄金比にもとづいたテクニカル指標に、フィボナッチ・リトレースメントがあります。
証券会社の株ツールによっては、利用できるようになっています。
リ・トレースメントとは、英語で綾戻しの意味。
株価チャートにおいて、起点と終点を設定すると、その間の61.8%、50.0%、38.2%等の位置を明示してくれる仕組みです。
株価におけるフィボナッチ・リトレースメント利用の例
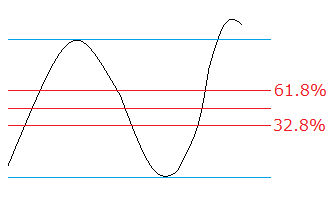
確かに比率が一目瞭然。
しかし、これで全てが上手く行くかと言うと、そんなことはありません。
使い方は自分で考えなければなりませんので。
フィボナッチ・リトレースメントの意味
起点・終点の位置を決めた時、フィボナッチ比率・黄金比による位置を明示してくれるのがフィボナッチリトレースメント。
つまり、基準を決めた時の相対的な位置の明示化。
言い換えれば、実際の話、基準を決めるのはトレードをする本人です。
フィボナッチリトレースメントのシステムが決めてくれる訳ではありません。
あなたが基準を決め、その基準に対応した相対的な位置が視覚化されただけ。
言えることは、自然界を支配し、世のあらゆる場所に現れるフィボナッチ数列。
この謎の黄金比率と、現実とのつながりを読み解く鍵。
それをあなたが握っているとも言えるのです。