テクニカル指標の効果
テクニカルが動けば、相場も上がる。
この界隈、そんなオカルト的言説が、そこかしこに行き交っています。
テクニカル指標は、そもそも役に立つのでしょうか?
株を始めた当初、当方はまず、MACDの魅力に取りつかれていました。
MACDの曲線を見ながら、買っていく。
どこかの雑誌にそう書いてあったのであります。
それを見たのは、2005年くらい。
ペラペラの薄い雑誌です。
この雑誌、結構流行っていました。
当方もやることが短絡的であります。
結果は言うまでもなく、惨敗。
正直に言いましょう。
テクニカル?
そんなことで儲かれば誰も苦労はしないのです。
常用テクニカル指標
そんな当方も、常に表示しているテクニカル指標があります。
エンベロープであります。
あくまで、チャートの縦横比・縮尺比をある程度一定にする。
そして移動平均線を一本だけ表示させておく。
そんな目的で使っているのみ。
これがなかなかシンプルでよろしい。
しかし、このおかげで儲かったと思った試しはありません。
テクニカル指標とは、その程度のものであります。
すなわち、チャートを見やすくし、イメージをつかむために使う。
なお、ボリンジャーバンドは使いません。
なぜなら、あれは一定の見方をしにくい、との判断。
ボリンジャーにおいて、チャートの縦横比・縮尺比が変わると、まったく別のイメージになってしまうのであります。
そもそも、ボリンジャーがスクイーズしたからと言って、何がどうなるわけでもありません。
当方の感触では。
2シグマ、3シグマに達したからと言って、相場がどうなるものでもなし。
そういう結論であります。
テクニカルの挫折
その後も様々なテクニカル指標に手を出しました。
ほとんど全て試したと言えるでしょう。
一目均衡、ストキャスティック、RSI、フィボナッチ、ピボットその他、ネットに出ているものはほぼ全て、やってみたのであります。
結論:やるだけ無駄。
無為な時間を過ごした末、テクニカル指標はオリジナルでなければダメなのではないか?
すなわち、一般的に使われていないテクニカル指標。
オリジナルを開発しなければならないのではないか?
そこで編み出したのが以下。
発行済株式数倍率
発行済株式数倍率とは、当方の造語。
この倍率が、とあるポイントを超えた時、株価は上がるのではないか?
そんな考えに取り付かれたのであります。
出来高に加え、別の要素を組み入れる、そんな発想で。
定義は、
発行済株式数倍率=当日の出来高÷発行済株式数
です。
これを各銘柄について割り出し、1を超えている、あるいはその近辺まで増加している銘柄を探し出します。
その目的のために、エクセルに全銘柄の発行済株式数を入力しました。
さて、エクセルに全市場・全銘柄の発行済株式数のデータを入れ込んだ当方。
銘柄コードを入力するや否や、発行済株式数倍率が瞬時に計算され、目の前にデカデカと表示されるシステムを完成させました。
これを見ながら、トレードを行うのです。
デイ・スイング、双方で試したこともあります。
テクニカルより怖いもの
当方、試行錯誤を続けました。
例えば、信用倍率・貸借倍率を上述のデータと絡み合わせるのであります。
結論的なことで言いますと、信用倍率・貸借倍率は、相場にさほどの影響を与えません。
買い残が多いから・売り残が多いから、だからどうたらこうたらと言う理論。
これで儲かった試しなし。
能書きを垂れるのに役立つ、と言うのはあります。
むしろ、大損しました。
上記システムで抽出した銘柄において、買い持ちしていたらいきなり増担保規制となり、爆下げを食らった、等であります。
信用倍率なんかより、東証の規制のほうがコワい。
あれ、やめてくれませんかね。
東証の規制は、一応の基準が公表されているとは言え、最終的には正確な予測は困難です。
運ゲー。
テクニカル不要論
テクニカル挫折後
本を数冊読んだところで、株取引の概要は若干わかるようになりました。
しかし、必勝法はどこにも書いてありません。
そのヒントすら書かれていないのです。
皆目見当がつかないまま。
その状態が1~2年くらいは続きました。
その間、日々、ツール上でチャートを見るようになり、様々なテクニカル指標を試しました。
テクニカルの経験則
今でもナンピンをやってしまうことがあります。
しかし、テクニカル指標は見ません。
移動平均だけは一応表示しています。
これは、ツールの仕様上勝手に表示されているだけ。
ほとんど当てにしていません。
なぜ当てにしていないかと言うと、何度もそれに頼って損をしているからです。
それ以外にも調べられ得る限りのテクニカル指標を試してみました。
今では株の本も読まなければ、日足チャートですら、あまり熱心には見ません。
相場の3要素
結論を言いましょう。
相場を解き明かす鍵は、
損益=f(x,y,z)
と言う式であります。
f(x)という表記は通常、関数を意味します。
関数とは、昭和初期までは函数と書かれていたと言います。
函とは箱と同義であり、fと言う名の計算機の箱に(Xの代わりに具体的な)数字をぶち込むと、計算されてその結果が出てくる。
その計算結果がf(x)であります。
カッコの中の数字は、変数。
f(x,y,z)とは、fと言う名の計算機に3つの具体的数字をぶち込み、自動的に計算された結果を意味します。
例えば、
F(1,2,3)=256
と書いてあったら、Fという計算機のx,y,zと言うカーソルに1,2,3をぶち込んだら、計算結果は256になりました、と言う意味です。
多変数関数って何?
f(x,y,z)のように、変数がx,y,zの3つある場合には、3変数関数と呼ばれます。
高校までの数学では、通常、1変数関数までしか扱ってはいけないことになっています。
文字の数はいくつ含んでいても構わないのですが、変数は一つだけに限定しなさい、と。
例えば、
(a+b)XY+abY+cZ
のような式は中学・高校でも出てきますが、あくまでも文字式としての扱いであって、XとYを変数として扱うことは、やるなと。
XとYを変数として扱うと、2変数関数ということになってしまい、高校数学の範囲から逸脱します。
(文字の数と変数を混同している人がいますが…。)
このため、高校でf(x)は見たことがあるけれど、f(x,y)は見たことがないと言う人が多いと思います。
f(x,y)やf(x,y,z)は、大学1~2年で習う範囲の数学だからです。
だから株のx,y,zって何よ
高校で多変数関数を扱う例外は、物理で出て来る波の式です。
f(x,t)などと言う表記が出てくることがあります。
xは位置、tは時刻を意味する2変数関数ですが、高校数学では扱ってはいけない範囲ですので、小さくしか出て来ません。
それで、当方流の相場の損益計算機である、f(x,y,z)ですが、xは株価、yは出来高、zは時刻。
何だよ、当たり前じゃないか。
数え切れないほどたくさんのテクニカル分析がありますが、その出発点になるのはこの3変数。
そう考えて以来、当方、テクニカルを一切見なくなりました。
時系列の株価と出来高、経過時間だけを見ていればそれで済むと。
そして、その3つを見ても何も浮かばないのであれば、テクニカル指標に頼って何かが見えたとしても、それは幻であると。
大損を防ぐための函
世の中の全ての事象は、それこそf(x1,x2,x3,…xn)と言う複雑怪奇なn変数関数です。
n → ∞ の極限値を求めて、世の中の問題を一挙に解決できれば、どんなにラクなことか。
相場の3変数、株価と出来高と時刻だけしか見ないのは、ファンダメンタルズその他の情報は短期売買には直接関係ないと思っているためです。
とは言え、大学レベル以上の数学を駆使してトレードしている訳でもありません。
そんな必要はないと気づきました。
3つの変数をぶち込む魔法の函さえ持っていれば。
自分独自の函を持つこと。
これが相場に必要なことなのであります。
相場の3次元
早い話、参照すべきデータが多すぎるのであります。
人間は3つくらいのことにしか注意力を回せません。
3つしか理解できない
私たちは、3つのことまでしか理解できないのであります。
それ以上のことについては、同時に注意力を向けることは困難。
例えば、信号は赤、青、黄の3色。
信号の青色は、実は青色ではなく緑色。
この程度のことを思い出せなかったとするなら、それが注意力の限界です。
ましてや、信号の色が5色も7色もあったら、混乱するばかり。
相場も同様であります。
各種テクニカルだけでたくさんあるのに、ファンダメンタルもあります。
利益剰余金、有利子負債、自己資本比率、営業キャッシュフロー、BPS、ROE、ROA、PER、PBR、騰落レシオ…。
いくらでもデータがあふれています。
これらを全て理解し、総合的に結論を出す?
なぜ3つしか頭に入らないのか
私たちが生活している場所は、3方向に広がる空間。
すなわち、3次元空間であります。
空間は3方向に広がる

自然界とは、この3次元空間そのものであります。
これに慣れ過ぎているため、3つ以上のことを同時に扱うのは難しいのであります。
認識できるのは3つだけなのか
3方向に広がる空間とは別の次元として、時間を1次元として数え、現実社会は4次元であると言う考え方もあります。
それ以外にも、次元を付け足し、n次元(nは任意の整数)を扱う考え方も存在します。
しかし、その考え方が自然界にそのまま適用できるのか否か、実証されてはいません。
誰も証明できていないのであります。
n次元を直感的に理解することは、ほとんど不可能です。
サイコロ型をイメージできない人間
私たちは展開図を見て、組み立てられた形がサイコロ型(立方体)になることを直感的に理解できます。
サイコロ型(立方体)の展開図
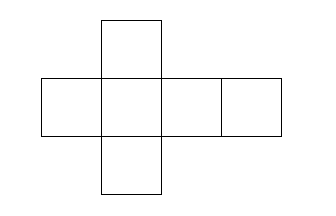
3次元空間に住んでいるため、完成した形状を簡単にイメージできるのであります。
しかし、2次元(平面)に住んでいる人間がいるとしたら、サイコロ型(すなわち立方体)を思い描くことはできません。
そんな場合、人は平面に閉じ込められた中で、無理矢理に展開図の辺と辺をくっつけようとします。
その結果、上記の展開図を組み立てた予想図として、以下のようなイメージを捻り出すことになります。
2次元に住む人間が考えるサイコロ型
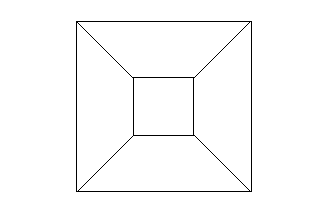
展開図の辺と辺を、平面内で無理矢理にくっつけると、この図になります。
これが2次元に住む人間が考え出すサイコロ型のイメージです。
平面内に閉じ込められて生きていたら、こんな結果にならざるを得ない。
聖杯の見つけ方
相場とは、平面に閉じ込められた人間と同じ。
3次元空間に生きる私たちも、n次元の図形(n≧4)を認識することは難しいのであります。
このn次元(n≧4)の世界、何とか図示することはできないでしょうか。
n個のデータを立体的に図示するのであります。
n次元空間の点を記録する方法。
そして、その結果、利益が出たポイントに色を塗っていきます。
コンピュータグラフィックスの得意な人に頼めばできるでしょう。
データが積みあがるにつれ、株の聖杯がどこにあるのかが明らかになります。
色が塗られたドットの集積として、相場の聖杯を明示することができるのです。
こんなふうに…。
聖杯のありか
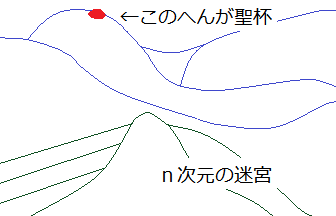
我々は、この相場空間において、ひたすら聖杯を手にするべく、n次元への旅路を続けているのであります。
さて、本日の結果は、スイング勝ち。
ほっと胸を撫でおろし、信用建玉を照会してみると。
若干含み損の銘柄があります。
若干?
それなら問題ないよな?
自分にそう言い聞かせました。
なぜ若干含み損なのか?
場中、その持ち株は寄り付いていません。
然るに含み損は増えてはいなかったのであります。
すなわち、当方、マウスをぶん投げ、キーボードを破壊し、壮大なちゃぶ台返しをしてわめく。
その日は明日へと持ち越しされました。
冷静なるままに。
ひとこと言わせてください。
「明日どうなっても知らんぞゴラ、ストップ高せいや!」
アレな株以外にク●株買い持ち。


